redivivaedizioni.com

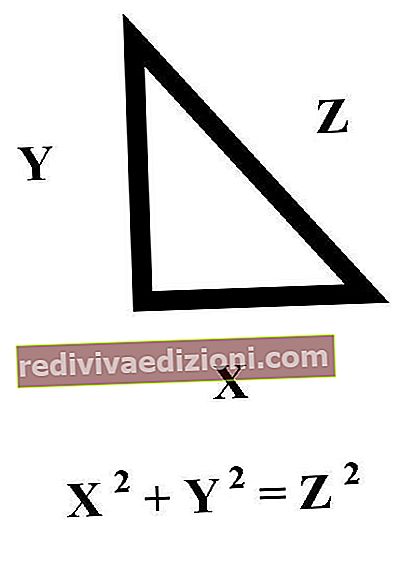정리는 수학의 필요와 특별한 관심사이며 , 이에 대해 이야기 할 때 논리적 프레임 워크 내에서 사실로 입증 될 수있는 진술을 참조 합니다.

일반적으로 정리는 미리 열거하거나 예상 할 수있는 여러 조건으로 구성되며이를 답변이라고합니다 . 그 다음에 결론 또는 수학적 진술이 나타날 것입니다. 이것은 분명히 문제의 작업 조건에서 항상 참일 것입니다. 즉, 정리의 유익한 내용에서 무엇보다도 확립 될 것은 사이에 존재하는 관계입니다. 가설과 논문 또는 작업 완료.

그러나 어떤 진술이 정리가 될 가능성이 있고 수학적 공동체 내에서 그리고 그것이 수학적 공동체를 위해 충분히 흥미로워 야 할 때 수학에 피할 수없는 것이 있습니다. , 결코 정리가 될 수 없습니다.

그리고 문제를 좀 더 명확히하기 위해서는 위에서 언급 한 개념을 구별하는 것도 필요합니다. 그래야 우리가 수학적 공동체의 일부가 아니더라도 그것이 정리, 기본형 인 경우를 인식 할 수 있습니다. 추론 또는 명제.

Lemma는 명제이지만, 더 긴 정리의 일부입니다. 그 부분에 대한 추론은 정리를 따르는 진술이며 마지막으로 명제는 특정 정리와 관련이없는 결과입니다.

처음에 우리는 정리가 논리 프레임 워크 내에서만 증명 될 수있는 진술이라고 지적한 반면, 논리 프레임 워크에서는 일련의 공리 또는 공리 시스템과 추론 프로세스를 참조하여 다음에서 정리를 도출 할 수 있습니다. 이미 도출 된 공리와 정리.

반면에, 잘 구성된 논리 공식의 유한 시퀀스는이 정리의 증명이라고 할 것입니다.

수학이 정리에 전념하는 특별한주의는 아니지만, 물리학이나 경제학과 같은 학문은 일반적으로 다른 사람으로부터 추론되고 정리라고도하는 진술을 생성합니다.